2.3.7/(1029/1024)：修订间差异

来自律学维基
跳转到导航 跳转到搜索
←上一编辑
可视化wikitext
无编辑摘要
 
（未显示2个用户的30个中间版本）
第1行： 第1行：
{{infobox ET}}
{| style="float:right; border:1px solid black; width:270px; background-color: #f0f0f0; border-collapse: collapse;"
!colspan="2" | 8/7-3ed3/2律
|-
! 子群
| style="background-color: #FFFFFF; font-weight: bold;" | 2.3.7
|-
! 音差
| style="background-color: #FFFFFF; font-weight: bold;" | 1029/1024
|-
! 映射
| style="background-color: #FFFFFF; font-weight: bold;" | [1 1 3; 0 3 -1]
|-
! 平均律
| style="background-color: #FFFFFF; font-weight: bold;" | 36 & 41
|-
! 生程
| style="background-color: #FFFFFF; font-weight: bold;" | 2/1, 8/7
|}
 
8/7-3ed3/2律是2.3.7子群上的规则调律，其生程为8/7, 三个8/7表示一个3/2, 四个8/7表示一个12/7.
 
== 调音 ==
假设生程2/1（八度）是纯的，则2.3.7/(1029/1024)的调音完全由8/7的调音决定。
 
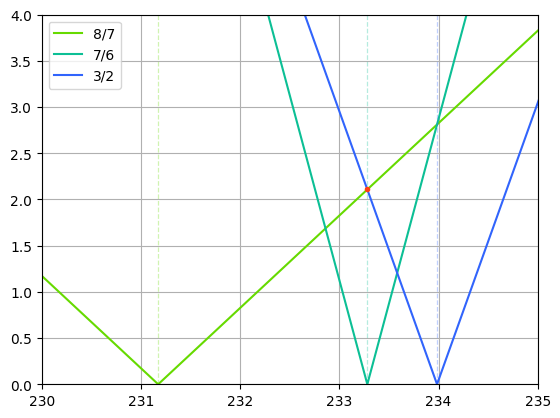
下图为8/7, 7/6和3/2的误差与8/7的调音的关系，其中横坐标为8/7的调音（[[音分]]值)，纵坐标为误差（音分值)，橙色点为最小化最大误差的调音，也就是1/4音差调音(8/7的调音为8/7 * (1029/1024)^(1/4)，3/2的调音为3/2 / (1029/1024)^(1/4), 7/6是准确的)，生程大小约为233.282¢.
 
[[文件:误差.png]]
 
== 和弦 ==
将8/7叠加三遍，可以得到1-8/7-21/16-3/2[[本质调和和弦]]，其相邻两音的音程为8/7，而根音与冠音之间的音程为3/2.
 
== 作品 ==
; Adriaan Fokker
* [https://www.huygens-fokker.org/music/rmten.html ''Tenacita'']
 
; Jan van Dijk
* [https://www.huygens-fokker.org/music/rmcap.html ''Capriccio'']
* [https://www.huygens-fokker.org/music/rmctta.html ''Canzonetta'']

2026年1月21日 (三) 14:32的最新版本

8/7-3ed3/2律
子群 2.3.7
音差 1029/1024
映射 [1 1 3; 0 3 -1]
平均律 36 & 41
生程 2/1, 8/7

8/7-3ed3/2律是2.3.7子群上的规则调律，其生程为8/7, 三个8/7表示一个3/2, 四个8/7表示一个12/7.

调音

[编辑 | 编辑源代码]

假设生程2/1（八度）是纯的，则2.3.7/(1029/1024)的调音完全由8/7的调音决定。

下图为8/7, 7/6和3/2的误差与8/7的调音的关系，其中横坐标为8/7的调音（音分值)，纵坐标为误差（音分值)，橙色点为最小化最大误差的调音，也就是1/4音差调音(8/7的调音为8/7 * (1029/1024)^(1/4)，3/2的调音为3/2 / (1029/1024)^(1/4), 7/6是准确的)，生程大小约为233.282¢.

和弦

[编辑 | 编辑源代码]

将8/7叠加三遍，可以得到1-8/7-21/16-3/2本质调和和弦，其相邻两音的音程为8/7，而根音与冠音之间的音程为3/2.

作品

[编辑 | 编辑源代码]
Adriaan Fokker
Jan van Dijk
检索自“https://tun.wiki/index.php?title=2.3.7/(1029/1024)&oldid=276”