|
|
| 第15行: |
第15行: |
| |- | | |- |
| ! 生程 | | ! 生程 |
| | style="background-color: #FFFFFF; font-weight: bold;" | 2, 8/7 | | | style="background-color: #FFFFFF; font-weight: bold;" | 2/1, 8/7 |
| |} | | |} |
|
| |
|
| '''Slendric''', alternatively and originally named '''wonder''' by [[Margo Schulter]]<ref>[https://yahootuninggroupsultimatebackup.github.io/tuning/topicId_76975.html#77043 Yahoo! Tuning Group | ''Music Theory (was Re: How to keep discussions on-topic)''], and [https://yahootuninggroupsultimatebackup.github.io/tuning/topicId_87455.html#88377 Yahoo! Tuning Group | ''The "best" scale.'']</ref>, or systematically '''gamelic''', is a [[regular temperament]] generated by [[8/7]], so that three of them stack to [[3/2]]. Thus the gamelisma, [[1029/1024]], is tempered out, which defines the [[gamelismic clan]]. Since 1029/1024 is a relatively small comma (8.4¢), and the error is distributed over a few intervals, slendric is quite an accurate temperament (approximating many intervals within 1 or 2 cents in optimal tunings).
| | == 调音 == |
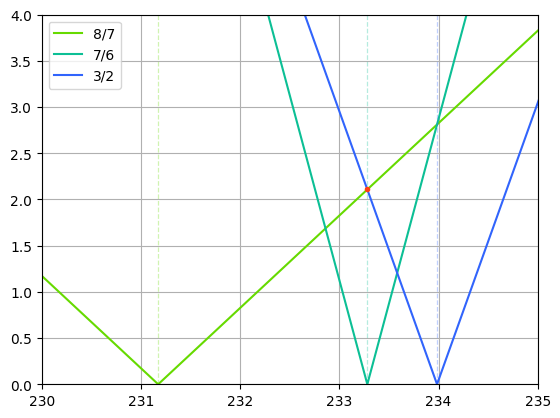
| | | 假设生程2/1(八度)是纯的,则2.3.7/(1029/1024)的调音完全由8/7的调音决定。下图为8/7, 7/6和3/2的误差与8/7的调音的关系,其中横坐标为8/7的调音([[音分]]值),纵坐标为误差(音分值),橙色点为最小化最大误差的调音,也就是1/4音差调音(8/7的调音为8/7 * (1029/1024)^(1/4),3/2的调音为3/2 / (1029/1024)^(1/4), 7/6是准确的)。 |
| The disadvantage, if you want to think of it that way, is that approximations to the [[5/1|5th]] [[harmonic]] do not occur until you go a large number of generators away from the unison. In other words, the 5th harmonic must have a large [[complexity]]. Possible [[extension]]s of slendric to the full [[7-limit]] include [[mothra]], [[rodan]], and [[guiron]], where mothra tempers out [[81/80]], placing 5/1 at 12 generators (4 fifths) up; rodan tempers out [[245/243]], placing 5/1 at 17 generators up; and guiron tempers out the schisma, [[32805/32768]], placing 5/1 at 24 generators (8 fifths) down. [[Weak extension]]s such as [[miracle]] and [[valentine]] are somewhat more efficient, but they change the generator chain.
| |
| | |
| From there, it is easy to extend these temperaments to the [[11-limit]] since 1029/1024 factorizes in this limit into ([[385/384]])⋅([[441/440]]), and so the logical extension of slendric is to temper out both commas; this places the interval of [[55/32]] at four generators up. Alternatively, giving 5/1 an independent generator and then tempering out 385/384 and 441/440 results in the rank-3 temperament [[portent]], the natural 11-limit [[expansion]] of slendric. Portent is [[support]]ed by the slendric extensions listed above.
| |
| | |
| This article concerns the basic [[2.3.7 subgroup]] temperament, slendric itself.
| |
| | |
| For technical data, see [[Gamelismic clan #Slendric]].
| |
|
| |
|
| [[文件:误差.png]] | | [[文件:误差.png]] |
| 8/7-3ed3/2律
|
| 子群
|
2.3.7
|
| 音差
|
1029/1024
|
| 映射
|
[1 1 3; 0 3 -1]
|
| 平均律
|
36 & 41
|
| 生程
|
2/1, 8/7
|
调音
假设生程2/1(八度)是纯的,则2.3.7/(1029/1024)的调音完全由8/7的调音决定。下图为8/7, 7/6和3/2的误差与8/7的调音的关系,其中横坐标为8/7的调音(音分值),纵坐标为误差(音分值),橙色点为最小化最大误差的调音,也就是1/4音差调音(8/7的调音为8/7 * (1029/1024)^(1/4),3/2的调音为3/2 / (1029/1024)^(1/4), 7/6是准确的)。